FINAL PROJECT : Anaylsis and Control of Car

Problem Statement :

Car is equiped with position sensor giving x,y co-ordinates of car. Initial orientation of car is known. Objective is to generate and track a trajectory of car given that no-slip condition is not satisfied if car goes beyond 25 m/s speed.

Approach :

There are two mathematical models are used in this project. 1) No-Slip Kinematic Model . 2) Drift Model . First one is used when velocity of vehicle is fairly low (25 m/s) while later one is used when veloctiy goes beyond 25m/s. Desired trajectory and control is generated using Direct Collocation which is done by using GPopsII software. Suitable backstepping controller is used to track the desired trajectory. Stability analysis using lyapunov method is presented. Extended Kalman Filter is used for observer. Finally system is tested for 4 different conditions to validate the model.

Mathematical Model of the system :

1) Kinematical Model

Position of center of mass of vehicle is denoted by x,y coordinates. There is position measurement sensor attached at C.M of vehicle with ,sensor covariance noise of for each x and y co-ordinates.

Constraints : Rear wheels can not have veloctiy in lateral direction as this model assumes no slipping of wheels.

Equations of Motion are given by,

Substituting into first two terms gives out,

Here velocity and steer angle are control inputs.

Controller Synthesis :

Using backstepping lets take and to be virtual control inputs such that,

Here zero dynamics of system is stable.

Now system becomes,

Backstepping inner loop is

Where and represents the desired trajectory.

We define a Lyapunov as,

Taking derivative,

choosing,

we get derivating of lyapunov to be always decreasing for positve gains

from system dynamic equations, we know and in terms of virtual controls, which is,,

inverting the matrix and substituting expressions of and , we get out controls,

As is always negative, controller is stable.

Observer Synthesis

We design Extended kalman filter for this non-linear system. Controller model requires only x,y co-ordinates to compute control inputs hence we need measurements from position sensor only. Thus observer can be used with controller model.

Discretizing,

and measurements,

where ,,, are noices in respective control signals or states.

, both are and , both are ..

Function file name EFK.m contains details of observer synthesis.

Controller Togather with Observer is applied here,

Drift Model :

In this model, each wheel is subjected to lateral frictional forces governed by Pacejka Magic Formula, an empirically derived formula which is used in simulation of vehicles in many applications.

where b,c,e depend upon tire cherecteristics, while k is slip angle to which henceforth we will call it .

Thus There are total 4 frictional forces acting in lateral direction of wheels. As front wheel have steering angle, lateral forces along them (i.e. F1, F2) change direction with change in steering angle. Equation of motion in fixed reference frame are given as,

Where

Simulations Experiments :

1. starting at rest and at origin. Need to reach (5,5) with orientation -pi/2 from positive y axis.

Trajectry Obtained from GPOPS

Trajectory Followed Using Controller (without noice in measurements) Controller 1

Trajectory Followed Using Controller (without noice in measurements) Controller 2

Kalman Filter with different control law on u2 given by,

u1 remains the same,

Using this law we can see orientation is matched but y are being sacrificed.

Comparsion of data :

comparision between Gpops and 2nd Controller,

comparisionAnalysis(time,states,time2,states2);

Trajectory Followed Using Controller after adding Extended Kalman Filter;

EKF();

2) Reverse

Trajectry Obtained from GPOPS

Trajectory Followed Using Controller :

Here we can see Controller follows slightly different trajectory.

comparisionAnalysis(time,states,time2,states2);

Using Kalman Filter, Tracked Trajectories :

EKF();

3) Parallel Parking

Trajectry Obtained from GPOPS

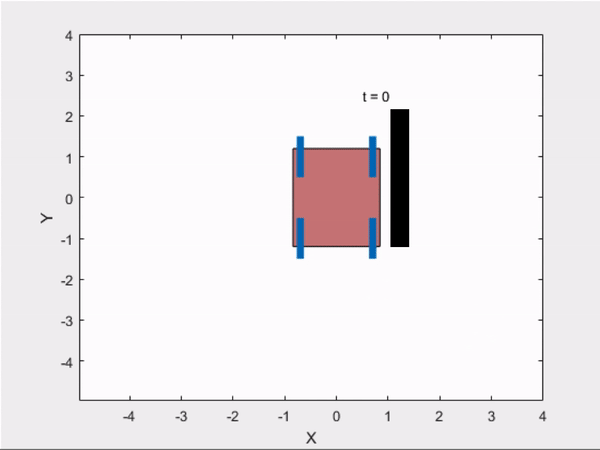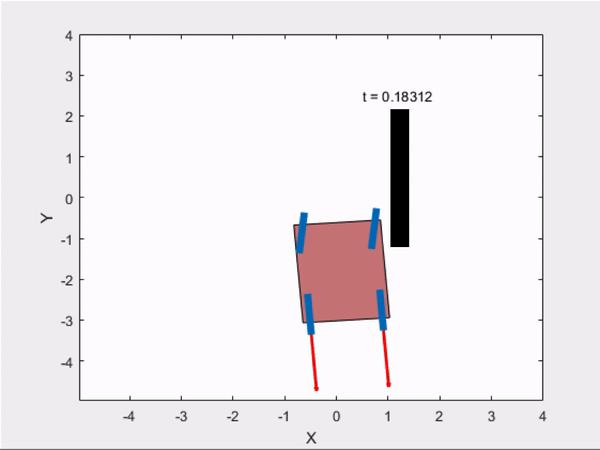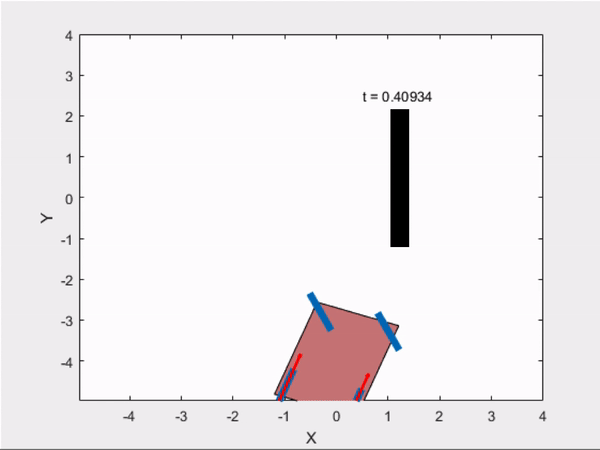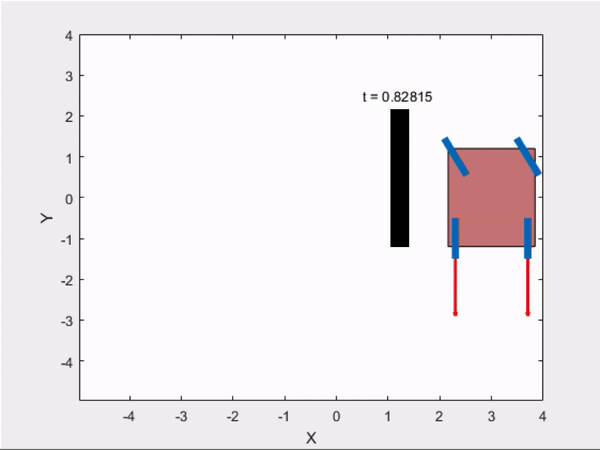
Trajectory Followed Using Controller :

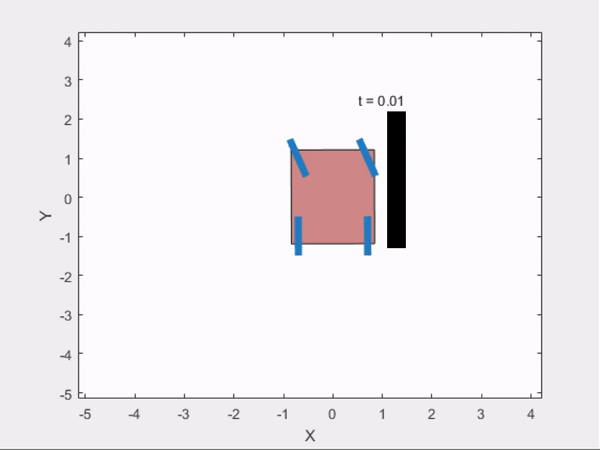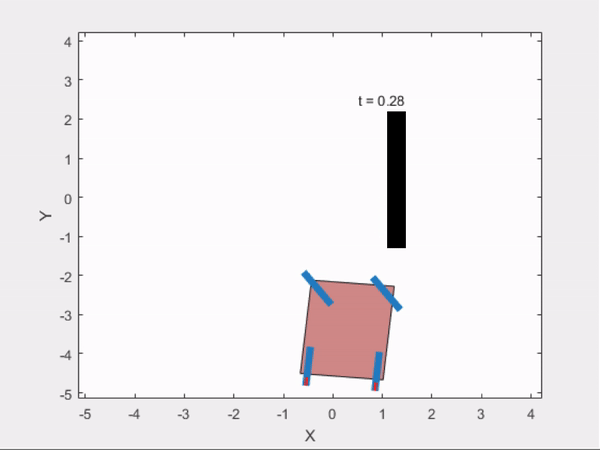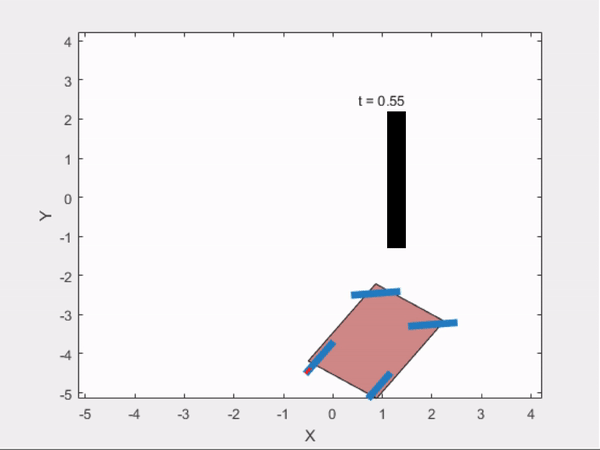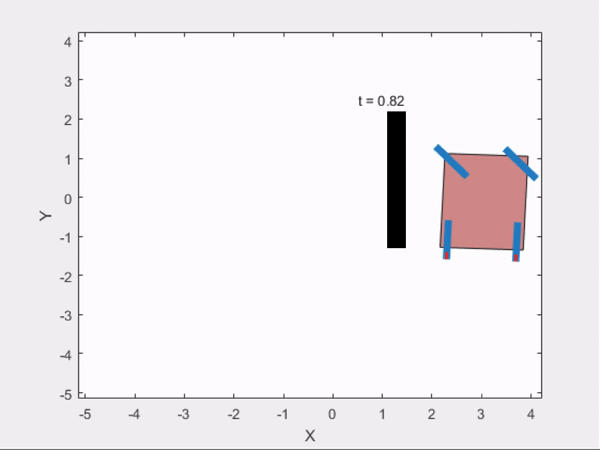
comparisionAnalysis(time,states,time2,states2);

Using Kalman Filter, Tracked Trajectories :

EKF();

4 ) Testing Environment 4 : With High Initial Velocity

Trajectry Obtained from GPOPS : (Drifting initially)

Trajectory Followed Using Controller : Here Controller miserably fails to get correct orientaion as car drifts initially. But system neverthless is stable.

comparisionAnalysis(time,states,time2,states2);

As one can see x, y are tracked with high accuracy but due to drifting orientation is mislead.

EKF();

Additional Findings

I could not find appropriate control method for controling vehicle with large drifting scenarios. But here is one interesting drifting turn that I found using GPoPs,

180 Turn of Car by drifting. (Those arrows indicate frictional forces)

Course Feedback :

1. I spent approximately 3 weeks . (Around 36 hours man hours)

2. I would try to apply neural network based control system for large drifting scenario, which I couldn't complete.

3. 1. Cover less material with increased depth.

3. 2 . If possible some hands on exercise on real devices.

4. 1. Nothing in life is to be feared, it is only to be understood

4. 2. Taking pride in what you do.

Self-Assessment

3. 1. Timeline handling

2. Presentation of work done

4. 1. Direct Collocation

2. Neural Network (Kick started at least)